
In the End, It All Adds Up to – 1/12, or does it?
Posted On:In the name of Allah, the Merciful to all, the Compassionate
Recently I watched a video clip in which two physicists from the University of Nottingham tried to prove that the sum of 1+2+3+4+5+... is equal to -1/12. At first I thought that it’s a joke, and it reminded me of a comedy classic in which Abbott proved that 13 x 7 = 28:
After further research, I found in Wikipedia that there are two 100 years old methods of zeta function regularization and Ramanujan summation which assign -1/12 to that series.
This is how they did the calculations:
Consider the following three sequences:
S1 = 1-1+1-1+1-1…
S2 = 1-2+3-4+5-6+7…
S3 = 1+2+3+4+5+6….
If we continue the sequence of S1 to infinity, we may get 0 or 1, depending on where we stop. The physicist claimed that there are calculation methods that prove the result is ½. Mathematically speaking we cannot conclude such a thing. Anyhow 0, 1, or ½ does not really change anything, and we should leave that subject for another time.
If we add S2 with S2, we have the following:
I shifted along the second S2, to add every two adjacent numbers. If you find the sum, you will find the result is:
2 x S2 = S1
If we assume S1= ½ then we can conclude that:
S2 = ¼
Now let’s find what S3 – S2 is going to be:
The result is equal to 4 x S3.
Then they concluded that:
S3 – S2 = 4 S3
If we take one S3 from each side, we have:
3 S3 = - S2 = - ¼
So S3 = - 1/12
What is wrong with this type of mathematics?
First let’s start with definition of infinity. By definition if we add or multiply to, or subtract from infinity, the result is still infinity. Let’s consider the following equation:
∞ = ∞ + 1
Can we take ∞ from both sides of equation and conclude that:
0 = 1 ???
Of course not; infinity should not be treated like natural numbers.
When the summation of a series is going to increase in each step and it’s not going to reduce, by definition the result is infinity, so the series of S3 is equal to infinity. If we subtract -1/4 from infinity, it’s still infinity. If we multiply it by 4, it’s still infinity. All we can conclude from S3 – ¼ = 4 S3 is:
∞ = ∞
All this hocus-pocus just shows the lack of understanding about the concept of infinity. The interesting part is this misunderstanding is at least 100 years old, and every new physics student thinks if it were wrong, his or her professors could catch it. Unfortunately they did not, and according to Wikipedia this calculation is used in String theory, computing the casimir force, and possibly many other theories. The claim of string theory about 26 dimensions of universe is driven from such shaky calculations.
Sorry physicists! If that type of mathematics is what you found your theories on, you are doomed.
The concept of infinity is abused a lot. For example, in calculation of the above-mentioned sequence of S2, the result is +∞ or -∞ , depending on when we stop the summation, and there is no reason for us to choose one of the results or average them. If the result is +∞, the result of adding S2 with S2 is +∞, and if it’s -∞, the result of addition is -∞ as well. So it’s not going to be equal to a finite number.


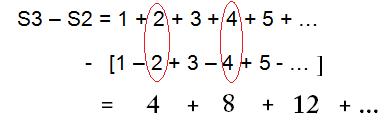
[…] در مقاله دیگری قبلاً درباره یک قضیه غلط ریاضی که حدود ۱۰۰ سال پیش مطرح شده بود، بحث کردهام. این قضیه غلط مبنای مباحث اولیه در نظریه String Theory و محاسبات Casimir forcee و بسیاری از نظریه های دیگر بوده است. آن مقالات اولیه و تمام مقالات بعدی که مقالات قبلی را مبنای خود قرار دادهاند هیچ اعتبار علمی ندارند. اگر این محاسبات غلط ریاضی را ریشهیابی کنیم و هر آنچه که بر مبنای آنها مطرح شده را کنار بگذاریم، تقریباً چیزی از فیزیک نظری باقی نمیماند. بقیه رشتههای علمی دیگر نیز کم و بیش دچار این مشکل هستند. […]